The TSTT sites have already developed significant mesh generation capability starting from geometric descriptions based on various representations. Unstructured mesh generation capabilities are provided by MEGA (RPI), CUBIT (SNL) [CUBIT] and NWGrid (PNNL); structured overlapping and hybrid mesh capabilities are provided by Overture (LLNL). To achieve true interoperability among the different mesh types, it is important that the mesh generation tools all operate on similar infrastructure and provide similar capabilities, and we have identified three areas that require improvement: meshes for high-order discretization techniques, mesh quality improvement, and mesh evolution.
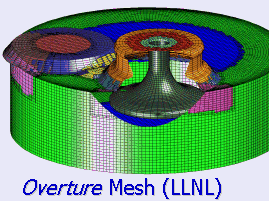

Figure 1. Meshes Generated Using TSTT Technology
Meshes for High-Order Discretization Techniques
First, many of our tools will be enhanced to support the high-order discretization techniques that will be provided as part of the Discretization Library; particularly in the case of complex geometries. Preserving the convergence rate for high-order discretizations over curved domains requires that the mesh elements themselves are curvilinear. Two functionalities needed to curve a straight-edge mesh are the geometric representation of curved mesh entities and the ability to modify the mesh to maintain mesh quality as the entities are curved to represent the portion of the boundary they cover. Alternative methods to define the element geometry for use in the discretization process have been examined and methods using approximating polynomials appear to be more effective than standard Lagrange interpolants. Research must be performed to determine the best ways to approximate geometry and to create the proper order curved mesh entities.
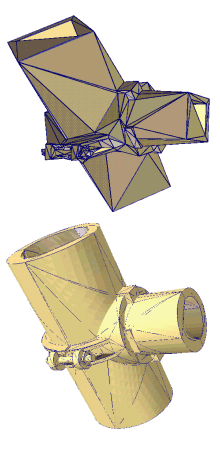
Figure 2. High order elements representing a curved domain (RPI)
Mesh Quality Improvement
Second, to ensure good quality hybrid meshes, we will develop stand alone mesh improvement tools that will work on all TSTT mesh types . Mesh quality and smoothness is critical for both the accuracy and efficiency of low- and high-order discretization techniques. For example, the solvers used in electromagnetics simulations for modeling linear accelerators and the hemodynamics simulations for studying vascular disease can be significantly impacted, sometimes failing to converge, unless mesh quality has been optimized. Although many algorithms exist to improve mesh quality, there currently exists no stand alone mesh improvement component that incorporates a broad spectrum of state-of-the-art approaches and that supports all of the TSTT mesh types. Such a software component will be critical to the success of the TSTT center for several reasons. First, we anticipate that mesh quality improvement algorithms will be needed for the transition regions in conforming hybrid meshes obtained from multiple meshing codes. This is especially true for high-order methods which employ relatively few macro-elements; the conditioning of the governing systems can be impacted significantly by the deformation of just a few elements. Second, both h-adaptivity and ALE r-adaptivity can significantly degrade mesh quality, which can be mitigated through the use of local mesh quality improvement algorithms. Research areas that will be pursued in this area include (i) a priori quality metrics appropriate for high-order discretization techniques and general polyhedral elements, (ii) a posteriori methods that use error indicators to drive optimization- based smoothing and flipping, and (iii) improvement algorithms for mixed/hybrid structured and unstructured meshes. All algorithms and software will use the low level common interfaces for accessing mesh geometry and topology described in the meshing section, hence, this stand alone tool will be compatible with all of the existing and proposed TSTT mesh generation tools. More information can be found in the mesh quality section.
Dynamic mesh evolution
In many applications, the mesh description of geometry evolves during a computation. Reasons for mesh evolution include adaptive mesh refinement/coarsening , internally tracked interfaces or fronts due to the simulation physics, or the motion of domain boundaries either in a prescribed fashion or in response to the simulation physics. These possibilities will be accommodated by the mesh hierarchy through the evolution of the hierarchy structure and the components at each level during a computation. Interfaces for communicating algorithmic or physical information to the underlying mesh generator and properly accessing and using the evolving mesh within an application simulation will be provided.
A significant amount of basic research will be done to provide interoperable adaptive techniques within the context of the mesh hierarchy described earlier. We consider adaptive procedures that account for mesh modifications locally (e.g., on an element-by-element basis), in selected subdomains, or in the entire domain employing information from the mesh hierarchy (see Figures 1 and 2). To accomplish the TSTT goals, we will develop adaptive techniques that address the following issues (described in more detail below):
- true geometry of the domain to preserve the convergence rates of high order discretization techniques,
- effective abstraction of adaptive analysis procedures to promote “plug and play” interoperability ,
- enhanced front tracking algorithms that are combined with hybrid mesh generation schemes to significantly improve accuracy,
- mesh modification procedures that account for multiple criteria to extend their applicability,
- mesh adaptation for hexahedral and mixed element meshes to provide equivalent capabilities among TSTT center tools, and
- automatic selection and application of optimal adaptive strategies to improve ease of use.
Accounting for the domain geometry during adaptive processes includes operations to ensure that refinements faithfully represent the original underlying geometry. In the case of straight edged geometry this includes new mesh vertices, while in the case of curved mesh entities it can include mesh vertices, edges, and faces. The process of conforming mesh entities to the boundary can invalidate elements or degrade them to the point of being unacceptable. In such cases it is necessary to apply mesh modification operators to problem elements. Procedures to perform such modifications for the full set of mesh and partition types supported by the TSTT center will be developed.
Most current adaptive procedures employ a tightly coupled error estimation and mesh adaptation strategy. To support the more effective insertion of various mesh adaptation procedures into alternative simulation procedures we will develop generalized mechanisms that accept error estimation and/or correction indication information as input and that determine the specific mesh adaptations to perform based on the available AMR procedures. These procedures will build on knowledge of the theoretical properties of the error, its control, and the relative computational cost of alternative strategies. Adaptive procedures for the accelerator, chemically reacting flows and biology applications, including those accounting for special constraints, such as grid alignment for the fusion application, will be considered early in the program.
Many classes of simulation are characterized by the formation of sharp fronts as the simulation evolves. In these cases, the most effective adaptive procedures must include a front tracking technique to accurately resolve the front. Exact conservation and higher order accuracy at the front are difficulties with present algorithms. Our studies indicate a significant improvement will result from addressing these two issues, for which purpose we will introduce a front adaptive, space-time discretization (instead of the more common space time semi-discretization). Three- dimensional meshes that are “swept” through time (including possible “collapses” and “splits” associated with dynamic bifurcation of the front topology) are required. Implementation of such space-time, front- adaptive meshes will be enabled by developing interoperability between our front-tracking code, FronTier, and the hybrid TSTT structured and unstructured mesh generation codes.

Figure 3. Meshes conforming to a sharp front
Interfaces developed to control adaptive simulation processes must consider cases in which multiple criteria drive adaptive mesh modifications. An obvious example where this is critical is in evolving geometry simulations based on Lagrangian meshes where mesh modifications are needed to maintain element shape control and mesh refinements are needed to control the discretization errors. One initial effort will be to consider the definition of the best refinement strategy for an element that is marked for refinement and also has one or more large dihedral angles needing reduction. We will develop generalized procedures that employ a full set of mesh modification operators (split, collapse and swaps) that account for both discretization error and shape improvement criteria.
Although effective mesh adaptation methods are known for unstructured tetrahedral meshes and overlays of structured grid sub-domains, general procedures are not available for unstructured hexahedral and mixed element meshes. For these mesh types, efforts will be taken to develop and compare adaptive refinement (both conforming and non- conforming) procedures and remeshing techniques using error size control maps.
